Comprender la recursión y la memorización mediante JavaScript

En este artículo, aprenderá a utilizar la programación recursiva, qué es y cómo optimizarla para su uso en algoritmos. Utilizaremos JavaScript como nuestro lenguaje de programación de elección para comprender el concepto de recursión.

Prerrequisitos

Usaré la notación Big O para comparar estrategias de optimización, que puedes repasar aquí.

¿Qué es la recursión?

La recursión se produce cuando una función se llama a sí misma dentro de sí misma, lo que puede crear un bucle infinito. Si alguna vez ha trabajado con animaciones de lienzo, entonces ya ha utilizado la recursión, ya que utilizamos una animatefunción que actualiza nuestra animación antes de volver a ejecutarse.

En el siguiente ejemplo, pasamos un número, lo duplicamos y luego pasamos ese valor a sí mismo nuevamente. En teoría, esto continuaría para siempre, pero debido a que las computadoras son limitadas, generalmente no podemos tener una recursión infinita. Obtendrá un error como too much recursiono Maximum call stack size exceededsi no incluye alguna condición de salida para detener la función, en el siguiente caso tan pronto como supere 100:

const double = num = {  num = num + num;  console.log(num);  if (num  100) return 'Exit'; // Try removing this  return double(num);};console.log(double(4));

Probablemente estés pensando: "Eso está muy bien, pero ¿no puedo usar un bucle para todo lo que pueda hacer la recursión?". Bueno, sí, pero en realidad no. La recursión resulta útil cuando se trabaja con varios algoritmos de búsqueda y ordenación o cuando se recorren estructuras de datos que son más complicadas que las listas simples. Cuando se hace correctamente, también se puede obtener un rendimiento mucho mejor, como O(log n) mientras que todos los bucles son O(n).

Memorización

No es necesario jugar mucho con la recursión para darse cuenta de que es bastante fácil sobrecargar el equipo. Esto se debe a que la mayoría de las funciones recursivas son O(n^2) o incluso O(n!). Dado que JavaScript se ejecuta en pilas de llamadas cada vez que se agrega una nueva capa recursiva, se debe utilizar una gran cantidad de memoria y potencia de procesamiento para administrarlo todo, a pesar de que la mayor parte es redundante.

Probemos algo sencillo, como generar una secuencia de Fibonacci. Una secuencia de Fibonacci es aquella en la que cada dígito es la suma de los dos elementos anteriores: 0, 1, 1, 2, 3, 5, 8, 12...

const fibonacci = num = {  if (num  2) return num;  return fibonacci(num - 1) + fibonacci(num - 2);};for (let i = 0; i  1000; i++) console.log(fibonacci(i)); // 3 minutes before page crashed...

Eso es simplemente horrible. Utilizar recursos para 1000 capas de la misma información es demasiado incluso para mi computadora, que es relativamente decente.

En lugar de eso, podemos solucionar este problema agregando una variable de almacenamiento, o un “memo”, que contendrá nuestros valores a medida que avanza la pila. Cada vez que se ejecute nuestra función, su valor se agregará a su índice correspondiente en el memo y la siguiente capa hará referencia a él para calcular nuestro resultado.

const fibonacci = (num, memo) = {  memo = memo || {};  if (memo[num]) return memo[num];  if (num  2) return num;  return memo[num] = fibonacci(num - 1, memo) + fibonacci(num - 2, memo);};for (let i = 0; i  1000; i++) console.log(fibonacci(i)); // 143 Milliseconds

Problema

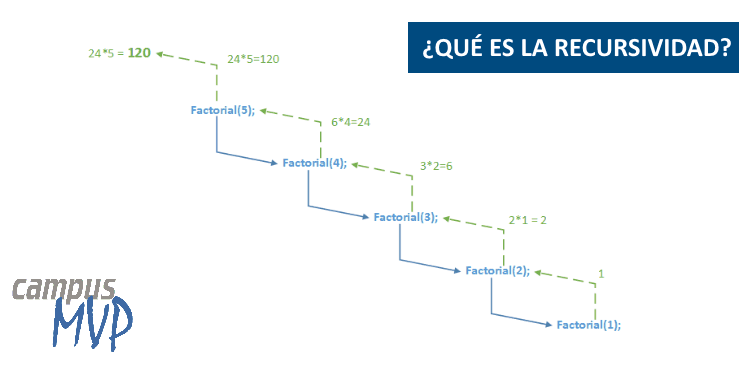
Intentemos aplicar esto a otra función recursiva. Esta toma un número y genera su factorial, por lo que 3! debería devolver 6 porque 3x2x1=6.

const factorial = n = {  let num = n;  if (n === 0) return 1;  for (let i = 0; i  n; i++) {    num = n * factorial(n - 1);  };  return num;};console.log(factorial(3)); // 7 Millisecondsconsole.log(factorial(6)); // 8 Millisecondsconsole.log(factorial(9)); // 15 Millisecondsconsole.log(factorial(12)); // 11,588 Milliseconds

Para mí, cualquier valor superior a 12 hace que la página se bloquee porque esta función tiene una complejidad de O(n!), ya que cada capa de la pila tiene que manejar la complejidad de la anterior.

En lugar de eso, intentemos memorizarlo y veamos la diferencia.

const factorial = (n, memo) = {  memo = memo || {};  if (memo[n]) return memo[n];  if (n === 0) return 1;  for (let i = 0; i  n; i++) {    memo[n] = n * factorial(n - 1, memo);  };  return memo[n];};console.log(factorial(12));  // 4 millisecondsconsole.log(factorial(120));  // 12 millisecondsconsole.log(factorial(1200)); // 24 millisecondsconsole.log(factorial(12000));  // 1408 milliseconds

No sé qué piensen ustedes, pero a mí me parece una mejora increíble: ahora puede realizar 10.000 cálculos en 1/8 del tiempo.

Reflexiones finales

La recursión es una de esas cosas con las que debes familiarizarte porque volverá repetidamente o te perseguirá a lo largo de tu carrera como programador. Será esencial para aprender a recorrer árboles y listas y ordenar varios conjuntos de datos en el futuro.